特殊算の代表選手と言えば「つるかめ算」ですね。鶴と亀の頭の合計が○個で足が○本です。鶴と亀はそれぞれ何匹いるでしょう?ってやつです。
問題
鶴と亀の頭の合計が10個で足の合計は34本でした。鶴と亀はそれぞれ何匹いるでしょう。
考え方
つるかめ算のポイントは、鶴と亀の足の数の差に着目することです。
つるは足が2本、かめは足が4本なので、その差は2本。この足の数の差が答えを導くポイントになります。
全てが亀だった場合を考える。
問題では、頭の合計が10個なので、全てが亀だった場合には「10(頭の数)×4(亀1匹あたりの足の数)」で足の数が40本になります。
足の数は34本なので全てが亀だと足の数が6本多くなってしまいます。
鶴と亀の足の数の差は2本なので、亀を1匹減らして、代わりに鶴を1羽増やすことで足の数は2本ずつ少なくなりますね。
全て亀だと足の数が6本多くなってしまうので、代わりに鶴を入れていくことで調整していきます。
6本多い足を、亀の代わりに鶴を入れていくことで2本ずつ減らしていくわけです。
亀を1匹外して鶴を1羽入れることで足の数を2本減らせるので、6本の足を減らしたいのなら「6÷2=3」ってことで亀を3匹外して鶴を3羽入れると足の数が合いますね。
頭の数が10個で、その内の3羽が鶴ということは、亀は「10-3=7」で7匹だということが分かります。
確認のために計算してみましょう。
鶴が3羽、鶴の足の数は1羽につき2本なので、鶴の足の数は全部で「3×2=6」で6本。
亀が7匹、亀の足の数は1匹に付き4本なので、亀の足の数は全部で「7×4=28」で28本。
鶴の足の数の合計6本と、亀の足の数の合計28本を足して「6+28=34」となるのでピッタリです。
答えは「鶴が3羽と亀が7匹」と出せました。
全てが鶴だった場合を考える。
問題では、頭の数の合計が10なので、その全てが鶴だった場合を考えてみます。
全てが鶴だった場合、10(頭の数)×2(鶴の1羽あたりの足の数)=20となります。
足の数の合計は34本なので、14本足りません。
鶴と亀の足の数の差は2(亀が2本多い)ので、鶴1羽外し、亀を1匹追加することで、足の数が2本ずつ増えていきます。
足りない足の数は14本なので、14(足りない足の数)÷2(鶴と亀を1ずつ入れ替えることで増える足の数)=7。
鶴を7羽外して、亀を7匹追加すると足の数が合う事がわかりました。
答えは、鶴3羽と亀7匹です。
面積図で考える
つるかめ算は、面積図で考えると解りやすいです。問題は「鶴と亀の頭の合計が10個で足の合計は34本でした。鶴と亀はそれぞれ何匹いるでしょう。」でしたので、図に表すと
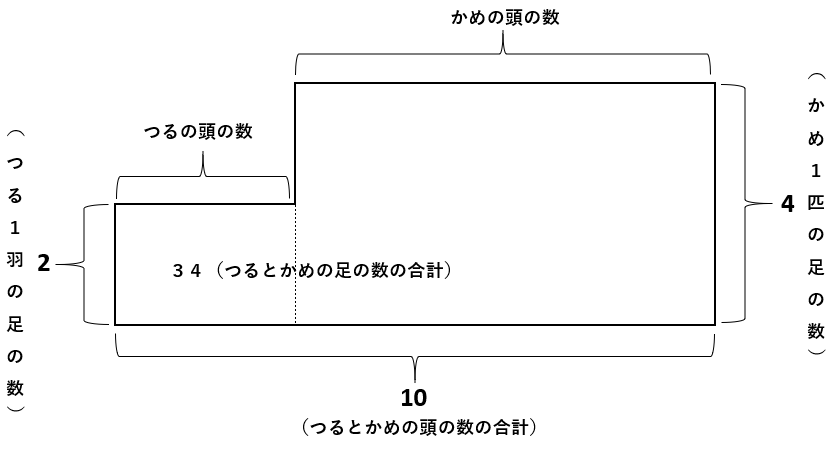
こんな感じになります。点線で区切られた左側が鶴の足の合計を表していて、右側が亀の足の合計を表しています。
問題では足の合計が34なので、左側と右側を足すと34になります。
次に、頭の数10個が全て亀だと仮定した場合の図を書いてみます。
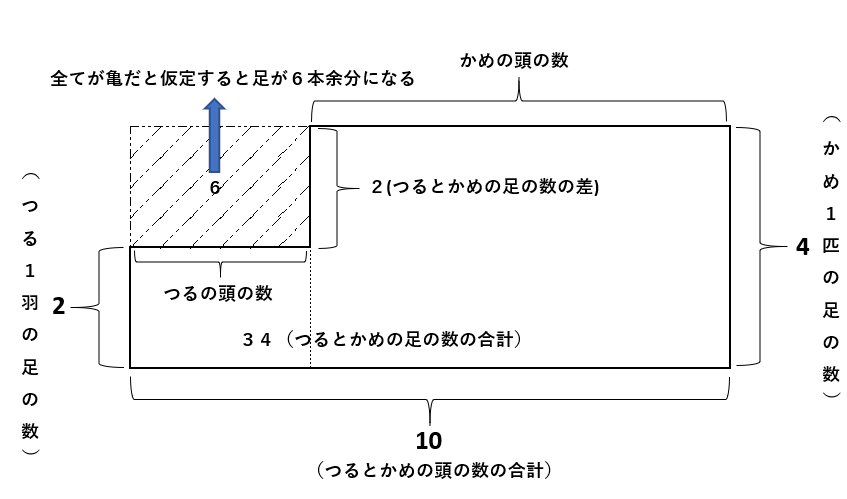
頭の数の合計10を全て亀だったと仮定すると、10(頭の数)×4(亀の1匹あたりの足の数)=40となります。
問題文では、足の数の合計が34なので、足の数が6本余ってしまっています(図の斜線部分が余った足の数)。
図の斜線部分の縦の長さは2(亀と鶴の足の数の差)なので、面積が6なら斜線部分の横の長さは、6(面積)÷2(縦の長さ)=3と求めることができます!
斜線部分の横の長さは鶴の頭の数なので、鶴の頭の数=3、亀の頭の数7(10-3)と答えにたどり着く事ができました。